## Z3Py：摘要
Z3Py 是微软研究院开发的高性能定理证明器，可通过 Python API 访问。它被用于软件验证、约束求解，甚至生物分析等多个领域。本指南介绍 Z3Py 的核心功能，无需预先了解 Python 知识（尽管鼓励学习 Python！）。
Z3Py 允许用户定义变量（整数、实数、位向量、布尔值）并表达约束。`solve()` 函数然后尝试找到满足这些约束的解。API 支持标准的数学运算和逻辑连接词。可以使用 `simplify()` 函数简化表达式。
主要功能包括：一个 `Solver` API，用于更精细地控制求解过程（逐步添加约束、检查可满足性，以及使用 `push` 和 `pop` 探索不同的场景），以及检查 Z3 找到的模型（解）。Z3 还支持未解释函数和常量，提供问题建模的灵活性。
除了基本的求解之外，Z3Py 还提供诸如位向量算术、列表推导式以简洁地定义问题，以及用于检查有效性和可满足性的函数等功能。它还可以用于模拟现实世界的问题，例如运动学方程和软件包安装冲突。
要在本地使用 Z3Py，请导入 `Z3` 模块并确保 Z3 Python 目录在您的 `PYTHONPATH` 中。
每日HackerNews RSS
这个Hacker News讨论围绕着Z3，一个强大的可满足性模理论（SMT）求解器。最初由一篇2015年的文章突出，展示了Z3在Python中解决诸如数独和N皇后问题等问题（尽管这篇文章现在已经过时），这次对话探讨了Z3的能力及其更广泛的影响。
用户指出，现代Python安装需要使用`pip install z3-solver`，而不是旧的`Z3Py`。Z3的优势在于它能够将复杂问题转化为布尔公式，利用现有算法并受益于持续的研究改进。它被用于各种领域，如程序验证、测试，甚至构建证明助手（如`knuckledragger`库）。
讨论还涉及了相关的工具，如CVC5，被认为同样强大，以及“SAT/SMT by Example”等资源，用于更深入的学习。一个关键的比喻将Z3描述为一个复杂的约束求解器，类似于通过逻辑推理和回溯来解决数独问题。
作者反思了在人工智能时代，像他们流行的 `blob-util` 包（每周超过 500 万次下载）这样的小型、实用型的开源库可能面临的衰落。虽然像 Claude 这样的工具现在可以轻松生成等效代码，从而消除了对外部依赖的需求，但作者质疑这样做会失去什么。 历史上，像 `blob-util` 这样的库具有双重目的：解决问题*和*通过周到的文档和示例来教育开发者。随着人工智能将即时解决方案置于理解之上，这种教学方面受到了威胁。这种转变也影响了创建这些小型库的动力，特别是当核心语言合并类似的功能时。 作者认为，未来的开源价值在于更大、更具创新性的项目，或者解决当前 LLM 训练数据之外的利基领域——例如复杂的调试技术。尽管存在担忧，他们仍然保持乐观，并以 Ripple.js 等项目为例，证明了人类持续的创造力以及不向人工智能让步的决心。最终，虽然 LLM 改变了格局，但它们并不会消除对所有开源贡献的需求。
## 简化 SQL 的 GROUP BY 子句 一项备受期待的 SQL 功能 `GROUP BY ALL` 正在接近标准化，以简化分组操作。目前，用户必须在 `GROUP BY` 子句中显式列出所有非聚合列，这对于复杂的查询来说可能既繁琐又容易出错。 `GROUP BY ALL` 会自动扩展以包含 `SELECT` 列表中的所有非聚合列。例如，`SELECT a, avg(b) FROM t1 GROUP BY ALL` 变为 `GROUP BY a`。但是，它*不会*自动处理更复杂的表达式；如果表达式包含聚合函数，用户仍然需要显式定义分组。 虽然 `GROUP BY ALL` 提供了便利，但也存在风险。对 `SELECT` 列表的更改可能会隐式地改变分组，从而可能导致意想不到的结果——类似于使用 `SELECT *` 的陷阱。因此，建议谨慎使用，尤其是在复杂或经常修改的查询中。 Oracle 和 PostgreSQL 等数据库中已经出现了实现，预计在 SQL 标准最终发布后，可用性将进一步提高。
## Hacker News 上关于 SQL 增强的讨论
一场 Hacker News 讨论围绕着 SQL 语言的改进建议，特别是关于灵活性和易用性。核心话题在于允许在 `GROUP BY` 和 `WHERE` 子句中引用别名和计算值——目前这通常是一个繁琐的过程，经常需要使用公共表表达式 (CTEs)。
用户指出，ClickHouse、PostgreSQL、DuckDB、BigQuery 和 Kusto 等数据库已经实现了类似的功能，例如按位置引用别名（例如 `GROUP BY 1`）或使用 `LET` 语句定义可重用变量。人们希望有一种更直观的语法，可能借鉴 LINQ 或 PRQL 语言中的概念。
SQL 工作组已经考虑了诸如 `ORDER BY ALL` 和 `SELECT * EXCEPT(col_name)` 之类的提案，后者可能会很快实现。然而，为了避免由于标识符作用域问题而破坏现有的 SQL 代码，更改会经过仔细评估。 讨论还涉及对可重用 CTE 定义（类似于视图）的需求，以及 `GROUP BY *` 的便利性。
此文档似乎是由Microsoft Word 2013于2019年9月5日创建的PDF文件。然而，文件的大部分内容由不可读、看似随机的字符和二进制数据组成——这是提取原始数据流的结果。 元数据表明它是由Word生成的，但主体不是人类可读的文本。文档可能包含复杂的格式、嵌入的对象，或者以某种方式损坏，导致将其视为纯文本流时出现乱码输出。本质上，根据其元数据，该文件*是*一个Word文档，但其内容无法以标准文本格式访问。
请启用 JavaScript 并禁用任何广告拦截器。
## 人工智能、隐私与不断变化的格局
这场 Hacker News 讨论围绕着一篇《Fast Company》的文章展开，该文章认为人工智能正在侵蚀隐私。用户们争论这是否是一个新问题，还是现有数据收集实践的更高效执行。
一个关键点是大型语言模型（LLMs）能够快速分析大量数据——包括个人互动——这些数据以前难以处理。这引发了人们对公司利用这种能力的担忧，可能破坏商业模式和用户对其数据的控制。有些人认为便利性胜过隐私问题，而另一些人则提倡本地的、用户控制的人工智能和数据存储作为解决方案，但硬件限制和应用程序设计障碍等实际挑战仍然存在。
几位评论员强调了一种历史模式：对新技术的最初热情往往掩盖了隐私考虑，一旦创新停滞，这种情况可能会逆转。人们对大型公司当前的“注重隐私”的实施持怀疑态度，认为它们优先考虑数据控制，而不是真正的用户所有权。最后，一位用户推广了一项名为 Verified Privacy AI 的新人工智能服务，旨在实现完全透明和隐私的密码学验证，但它立即面临对其自身数据收集实践的批评。
随着芯片越来越强大和集成度越来越高，散热问题日益严重，正威胁着计算的未来。半导体行业正在探索激进的解决方案，以防止过热和潜在的停机，这对于下一代3D芯片和人工智能等 demanding 应用尤其重要。 目前的方法包括先进的液体冷却——利用水-乙二醇混合物、介电液体，甚至将服务器浸入沸油中——但这些方法成本高昂且复杂。更有创新性的技术也在涌现：激光冷却，它将热振动转化为可移除的光子，以及用多晶金刚石薄膜涂覆晶体管以实现高效散热。 这些解决方案并不便宜，但人工智能领域源源不断的需求正在推动对这些以前难以想象的技术的投资。最终，跟上摩尔定律和现代计算不断升级的电力需求，将需要采用昂贵、尖端的散热管理技术。
黑客新闻 新 | 过去 | 评论 | 提问 | 展示 | 招聘 | 提交 登录
钻石和激光：芯片散热管理 (ieee.org)
14 分，来自 rbanffy 1 天前 | 隐藏 | 过去 | 收藏 | 讨论
指南 | 常见问题 | 列表 | API | 安全 | 法律 | 申请YC | 联系
搜索：
## AI 产品现状 (2025) 尽管投入了大量资金，但 AI 产品领域却出乎意料地狭窄。目前，只有三种类型的产品被证明是*有效*的：**聊天机器人**（如 ChatGPT，尽管是一个通用解决方案，但仍然占据主导地位）、**补全工具**（如 GitHub Copilot，提供智能自动补全——尤其在编码方面取得成功）和**代理**（在收到单个提示后自主执行任务，最近得益于 Claude Sonnet 等先进模型）。 大多数“新型 AI 产品”仅仅是聊天机器人，难以与 ChatGPT 等基础模型提供的广泛功能竞争。试图向聊天机器人添加“工具”的尝试，常常因用户操纵（“越狱”）而失败。 虽然存在利基市场（如明确的角色扮演聊天机器人），但这些市场可能会被大型 AI 实验室所取代。新兴的可能性包括**AI 生成的信息流**（个性化内容流，目前 Meta 和 OpenAI 等公司正在大力投资）和**AI 驱动的游戏**，但后者面临开发障碍和游戏玩家的抵制。 关键在于，成功的 AI 产品尽可能避免直接的聊天机器人交互。补全工具和代理在*无需*用户“与”AI“交谈”的情况下提供价值。未来可能出现特定领域的代理（如法律或医学研究工具），并且，AI 驱动的内容流有可能成为我们与互联网交互的主要方式。
## AI 产品格局：批判性观察
这次 Hacker News 的讨论围绕着一篇对成功的 AI 产品进行分类的文章展开，引发了对其关注范围过于狭窄的争论。原始作者确定了三种可行的类型：**聊天机器人**（如 ChatGPT）、**代码补全工具**（Copilot）和**代理工具**（Claude Code），并认为 AI 生成的信息流和游戏未来可能取得成功。
然而，评论者认为这忽略了许多*已经*成功应用的 AI 应用。引用的例子包括 **Grammarly、Deepl、文档解析工具、图像/视频生成（超越聊天机器人）以及现有软件中的 AI 驱动功能**，如 Adobe 产品。一个关键点是，许多有价值的 AI 应用是在*幕后*运作的，通过改进流程而无需直接用户交互。
讨论强调了对以 LLM 为中心的 AI 观点存在偏见，并质疑当前对“代理”的炒作是否准确反映了更广泛的 AI 格局。许多人认为 AI 的真正价值在于增强现有工作流程和解决特定问题，而不是完全取代人类任务。人们也对强大的 AI 代理的伦理影响以及潜在的滥用可能表示担忧。最终，这场对话表明，需要对 AI 的当前和未来影响进行更细致的观察。
傅里叶变换
Fourier Transforms
10 天前
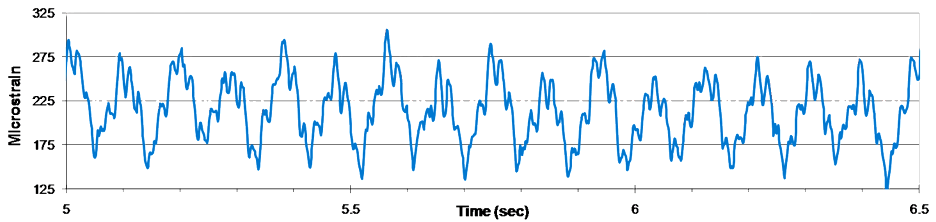## 傅里叶变换的误用风险
傅里叶变换（FFT）是一种强大的工具，但经常被误用和误解，甚至包括技术专家。 核心问题在于，人们将FFT视为揭示数据内在真相，而不是将其识别为曲线拟合过程——具体来说，是拟合正弦和余弦波。
这会导致错误的结论。 仅仅因为FFT显示了一个频率分量，并不意味着原始信号*实际*在该频率下振荡。 作者通过例子说明了这一点：非整数个正弦波周期显示为多个频率，以及由于长时间窗口内的数据漂移而产生的“幻影”频率。
关键在于理解FFT提供的是*什么*：构成正弦波的振幅和相位。 重要的是，图表通常只显示幅度，省略了重要的相位信息。准确的解释需要考虑数据的背景——分析窗口是否与信号的周期同步？瞬态因素是否影响了结果？
从轮胎变形分析到直升机振动研究，作者强调FFT是实现目的的一种手段，而不是目的本身。 仔细审查和理解基本原理对于避免从这些普遍分析中得出错误的结论至关重要。
关于 新闻 版权 联系我们 创作者 广告 开发者 条款 隐私政策和安全 YouTube 工作原理 测试新功能 © 2025 Google LLC