鲍勃·韦尔,感恩而死乐队的联合创始人,在与肺部问题斗争后去世,享年78岁,此前他曾成功战胜癌症。作为一名歌手、词曲作者和吉他手,韦尔的音乐帮助将感恩而死乐队打造成了一个持续了60年的音乐力量。他常常被杰里·加西亚的光芒所掩盖,却是乐队独特声音中至关重要、不显眼的一部分——其特点是椭圆形的riff和即兴风格。 韦尔出生于旧金山,在湾区长大,1965年与加西亚相遇,组成了“战魔”(The Warlocks),后来更名为感恩而死乐队。他克服了早期的挑战,包括与成瘾作斗争和在音乐上被边缘化的时期,最终成为乐队的关键主唱和词曲作者,创作了像“Playing in the Band”和“Cassidy”这样的经典歌曲。 在加西亚1995年去世后,韦尔继续巡演并通过各种形式来维护乐队的遗产,包括与约翰·梅耶合作的Dead & Company,最终在2023年完成了最后一次巡演。他始终致力于确保感恩而死乐队的音乐能够流传下去,认为它是一种共同的语言和社区。他在2024年8月在金门公园的最后一场演出标志着他“漫长而奇特的旅程”的结束。
每日HackerNews RSS
## 铁氧体:一款轻量级原生编辑器
铁氧体是一个用 Rust 和 egui 构建的快速轻量级文本编辑器,专为 Markdown、JSON、YAML 和 TOML 文件设计。它主要为 Windows 开发,但也支持 Linux 和 macOS(测试较少)。
主要功能包括具有实时预览的所见即所得 Markdown 编辑器、用于结构化数据的树形视图、具有正则表达式的强大查找和替换功能,以及完整的撤销/重做功能。用户可以受益于拆分视图、禅模式、40 多种语言的语法高亮、代码折叠、小地图和括号匹配。
铁氧体支持工作区模式,具有文件树和快速切换器,以及显示文件状态的基本 Git 集成。它提供会话持久性、浅色和深色主题、文档大纲和导出为 HTML 的功能。高级功能包括用于 shell 命令的实时管道和原生图表渲染(流程图、序列图等)。
铁氧体可供 Windows、Linux 和 macOS 下载,优先考虑原生、响应迅速的体验,并提供可自定义设置,欢迎社区贡献。
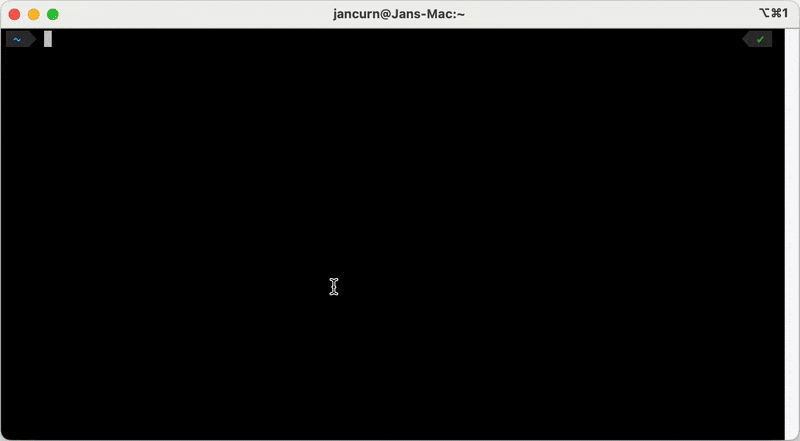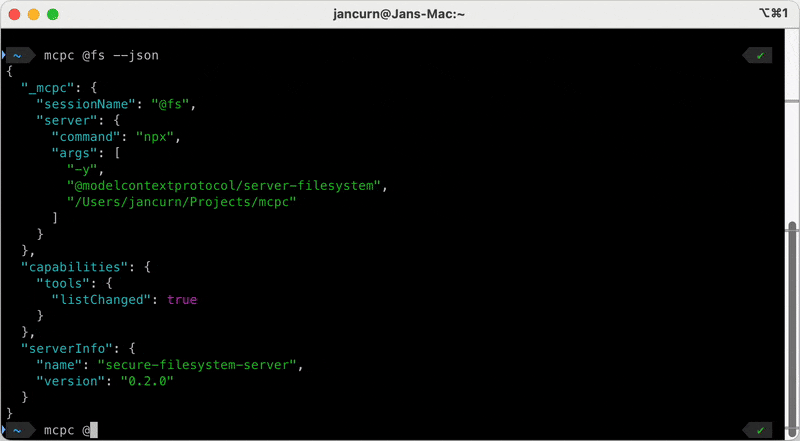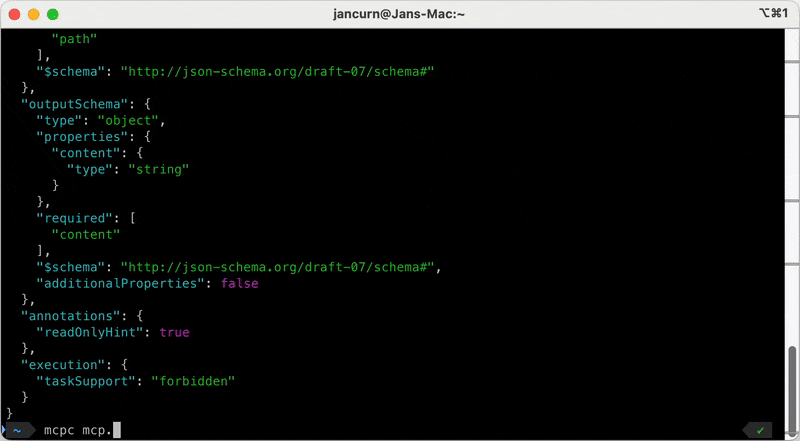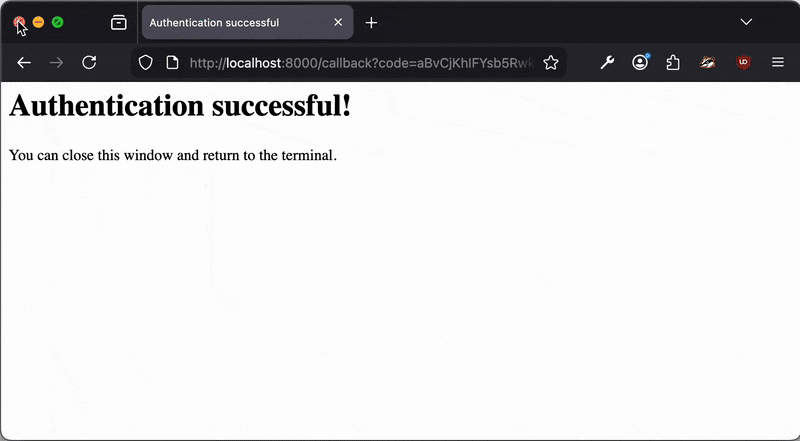 ## mcpc:模型上下文协议 (MCP) 的命令行客户端
`mcpc` 是一款功能强大的 CLI 工具,用于与 MCP 服务器交互,为 shell 使用、脚本编写和 AI 代理提供流畅的体验。它通过直观的命令简化 MCP 操作,支持持久会话,并启用“代码模式”,方便使用 `jq` 等工具进行脚本编写。
**主要特性:**
* **通用兼容性:** 通过 Streamable HTTP 或 stdio 与任何 MCP 服务器兼容。
* **持久会话:** 管理多个活跃的服务器连接。
* **安全:** 支持带有操作系统密钥链凭证存储的 OAuth 2.1,并为 AI 代理提供可选的基于代理的沙盒。
* **脚本友好:** JSON 输出支持与脚本语言集成。
* **AI 沙盒:** 为 AI 生成的代码创建安全的代理,以访问 MCP 会话。
* **全面的 MCP 支持:** 包括用于检查服务器、管理工具/提示/资源以及记录的工具。
**用法:** `mcpc [选项] <目标> [命令]`,其中 `<目标>` 可以是服务器 URL、命名会话或配置文件中的条目。命令包括 `tools-list`、`tools-call`、`prompts-list` 和 `shell`,用于交互式探索。
**安装:** `npm install -g @apify/mcpc`。Linux 用户可能需要安装 `libsecret-1-0` 以进行安全的凭证存储。
`mcpc` 旨在成为一个强大而安全的接口,以利用模型上下文协议的功能。
## mcpc:模型上下文协议 (MCP) 的命令行客户端
`mcpc` 是一款功能强大的 CLI 工具,用于与 MCP 服务器交互,为 shell 使用、脚本编写和 AI 代理提供流畅的体验。它通过直观的命令简化 MCP 操作,支持持久会话,并启用“代码模式”,方便使用 `jq` 等工具进行脚本编写。
**主要特性:**
* **通用兼容性:** 通过 Streamable HTTP 或 stdio 与任何 MCP 服务器兼容。
* **持久会话:** 管理多个活跃的服务器连接。
* **安全:** 支持带有操作系统密钥链凭证存储的 OAuth 2.1,并为 AI 代理提供可选的基于代理的沙盒。
* **脚本友好:** JSON 输出支持与脚本语言集成。
* **AI 沙盒:** 为 AI 生成的代码创建安全的代理,以访问 MCP 会话。
* **全面的 MCP 支持:** 包括用于检查服务器、管理工具/提示/资源以及记录的工具。
**用法:** `mcpc [选项] <目标> [命令]`,其中 `<目标>` 可以是服务器 URL、命名会话或配置文件中的条目。命令包括 `tools-list`、`tools-call`、`prompts-list` 和 `shell`,用于交互式探索。
**安装:** `npm install -g @apify/mcpc`。Linux 用户可能需要安装 `libsecret-1-0` 以进行安全的凭证存储。
`mcpc` 旨在成为一个强大而安全的接口,以利用模型上下文协议的功能。
1970年春天,巴黎市和FNAC合作举办了一项雄心勃勃的摄影比赛。目标是什么?通过将城市划分为1755个250米见方的网格,创建一份全面的巴黎摄影记录。 超过15,000名业余摄影师参与,其中2,800人提交了完整的作品集。这些照片随后捐赠给了巴黎市历史图书馆,在那里被数字化并整理成一个可公开访问的在线收藏。 如今,该收藏拥有来自6918位贡献者的超过30,225张数字化照片。目前的网站允许用户快速查看在特定250米网格内拍摄的所有照片,并链接到图书馆网站上的高分辨率版本。这是一份独特的1970年巴黎视觉快照。
一项来自布朗大学的新研究显示,全美自闭症治疗中心中的私募股权投资大幅增加。过去十年里,各公司已收购42个州的574家中心,其中近80%的收购发生在2018年至2022年间。 研究人员发现,投资集中在自闭症患病率较高且保险覆盖范围较宽松的州。私募股权的快速涌入引发了人们对利润优先于患者护理的担忧,可能导致治疗强度增加(且可能不必要),并给州医疗补助预算带来压力。 该研究强调了这些收购缺乏透明度,因为私募股权公司没有义务公开披露收购信息。研究人员目前正在寻求资金,以调查私募股权所有权对治疗效果、护理可及性和自闭症儿童服务整体质量的影响。目标是确定这项投资是否真正改善了护理,还是主要由财务收益驱动。
 ## Tux Paint:一款有趣且免费的绘画工具
Tux Paint 是一款备受喜爱、屡获殊荣的绘画程序,专为 3-12 岁的儿童设计,但同样受到成年人的喜爱!它在全球学校中广泛使用,通过其简单的界面、有趣的音效和可爱的企鹅吉祥物来培养计算机素养和创造力。
该程序提供一个空白画布和各种艺术表达工具。除了主要用户群体外,Tux Paint 还因其特殊效果而受到“故障艺术”爱好者的欢迎。
Tux Paint 免费提供在众多平台使用,包括 Windows、macOS、Linux、Android,以及现在(非官方)的 iOS。它是一款开源且无广告的软件,这使其成为学校和家庭可访问的资源,无需购买或预算审批。由志愿者开发,Tux Paint 旨在通过易于访问的数字艺术来激发创造力和分享。
## Tux Paint:一款有趣且免费的绘画工具
Tux Paint 是一款备受喜爱、屡获殊荣的绘画程序,专为 3-12 岁的儿童设计,但同样受到成年人的喜爱!它在全球学校中广泛使用,通过其简单的界面、有趣的音效和可爱的企鹅吉祥物来培养计算机素养和创造力。
该程序提供一个空白画布和各种艺术表达工具。除了主要用户群体外,Tux Paint 还因其特殊效果而受到“故障艺术”爱好者的欢迎。
Tux Paint 免费提供在众多平台使用,包括 Windows、macOS、Linux、Android,以及现在(非官方)的 iOS。它是一款开源且无广告的软件,这使其成为学校和家庭可访问的资源,无需购买或预算审批。由志愿者开发,Tux Paint 旨在通过易于访问的数字艺术来激发创造力和分享。
汉斯·霍尔拜因年轻,一位德国艺术家,很大程度上塑造了人们对都铎王朝的持久视觉印象。伊丽莎白·戈德林的研究传记揭示了一个比亨利八世及其宫廷画像画家更为复杂的人物。霍尔拜因以捕捉肖像对象的心理深度而闻名——这在当时是一种新颖的做法——但他也是一位多才多艺的工匠,为从珠宝到教堂装饰等各种物品设计。 受到瑞士宗教动荡的推动,霍尔拜因于1526年移居英格兰,最初通过与伊拉斯谟和托马斯·莫尔的关系,最终成为御用画家。戈德林展示了他的适应能力,强调了他如何应对宗教改革和不断变化的政治局势,优先考虑委托和赞助人。 尽管创作了亨利八世的标志性形象,但霍尔拜因为国王绘制的肖像仅存一幅。该传记一丝不苟地重建了已失传的作品,并探讨了霍尔拜因广泛的网络,甚至暗示他在情报收集方面的作用。戈德林将他描绘成一个务实的“工作狂”,将宗教艺术传统融入世俗委托,最终,他是一位适应性大师,而不是一位传统意义上被赞扬的“艺术家”。这本图文并茂的传记为艺术史上一个关键人物提供了引人入胜且细致入微的画像。
## 从可知到不可知:信息时代的新偏见 数十年以来,“可得性启发法”——通过例子容易想到的程度来判断可能性——塑造了我们的思维。在信息有限的时代,这是一种合理但并不完美的捷径。然而,如今的信息*过剩*已经改变了局面,产生了一种新的偏见:**不可得性偏见**。 我们不再关注*容易*获取的信息,而是专注于*应该*可见但实际上不可见的信息,将其缺失解读为虚假或阴谋的证据。这源于对数字时代完全透明的期望。例子包括因为缺乏预期的图像而质疑合法的法律程序,因不熟悉的情况而导致的医疗误诊,甚至缺乏与媒体叙事“契合”而被忽视的想法。 这种偏见不是源于无知,而是一种危险的缺乏*认识论谦逊*——拒绝承认我们不知道的事情。为公平和正当程序而设计的机构,现在因为*不*提供即时可见性而受到怀疑。最终,不可得性偏见会导致系统性的错误决策和对现实的扭曲认知,未被看到的事实被视为不存在。
启用 JavaScript 和 Cookie 以继续。
![]() Fly.io 认为当前标准的代理隔离方式——只读沙箱已经过时。他们构建了“Sprites”,这是一种持久的、快速配置(1-2秒)的“一次性云计算机”,具有100GB存储空间,旨在解决瞬态沙箱的局限性。与每次使用后都会重置的沙箱不同,Sprites 可以持久存在,允许代理保持状态并避免代价高昂的重新初始化。
核心论点集中在像 Claude 这样的人工智能代理的需求上,这些代理不适合无状态容器环境。这些代理受益于持久存储以及在无需不断重建的情况下演化代码和环境的能力。Sprites 提供一流的检查点和恢复功能,能够在约 1 秒内从错误中快速恢复。
Fly.io 设想未来代理可以访问完整的“计算机”,而不仅仅是受限的沙箱,从而实现更复杂、更高效的工作流程。他们相信这种转变将赋予更广泛的用户——超越专业开发人员——直接构建和定制应用程序的能力,模糊开发和生产之间的界限。最终,他们认为沙箱时代已经结束,未来在于像 Sprites 这样易于获取、持久且一次性的计算资源。
Fly.io 认为当前标准的代理隔离方式——只读沙箱已经过时。他们构建了“Sprites”,这是一种持久的、快速配置(1-2秒)的“一次性云计算机”,具有100GB存储空间,旨在解决瞬态沙箱的局限性。与每次使用后都会重置的沙箱不同,Sprites 可以持久存在,允许代理保持状态并避免代价高昂的重新初始化。
核心论点集中在像 Claude 这样的人工智能代理的需求上,这些代理不适合无状态容器环境。这些代理受益于持久存储以及在无需不断重建的情况下演化代码和环境的能力。Sprites 提供一流的检查点和恢复功能,能够在约 1 秒内从错误中快速恢复。
Fly.io 设想未来代理可以访问完整的“计算机”,而不仅仅是受限的沙箱,从而实现更复杂、更高效的工作流程。他们相信这种转变将赋予更广泛的用户——超越专业开发人员——直接构建和定制应用程序的能力,模糊开发和生产之间的界限。最终,他们认为沙箱时代已经结束,未来在于像 Sprites 这样易于获取、持久且一次性的计算资源。