本文探讨了德古阿定理及其向更高维度的推广,并用Python代码进行了演示。德古阿定理(1783年)指出,对于三个相互垂直的面在顶点相交的四面体,第四个面的面积平方 (A0²) 等于其他三个面的面积平方之和 (A1² + A2² + A3²)。提供的Python代码计算四面体各面的面积并验证该定理,打印结果非常接近于零。 然后,本文将这个概念扩展到4-单纯形(四面体的4维等价物),并展示了一个类似的涉及体积的关系 (V0² = V1² + V2² + V3² + V4²)。再次使用Python代码计算这些体积并确认该定理,尽管存在浮点算术的限制,但结果仍然接近于零。 最后,它讨论了小的数值误差的来源——几乎相等数字的相减,这导致浮点计算中精度损失。
每日HackerNews RSS
客户端挑战:您的浏览器已禁用 JavaScript。请启用 JavaScript 以继续。网站的必要部分无法加载。这可能是由于浏览器扩展、网络问题或浏览器设置造成的。请检查您的连接,禁用任何广告拦截器,或尝试使用不同的浏览器。
## 随机数据反汇编:Zig & Capstone 实验
该项目调查了随机字节流是否比未压缩的 Thumb 指令更有可能包含有效的 DEFLATE 压缩的 ARM (Thumb 模式) 指令,以解决一次友好的争论。作者假设由于 Thumb 的高代码密度,随机字节形成有效的未压缩 Thumb 代码的概率更高。
使用 Zig 和 Capstone,作者生成了随机字节序列,尝试直接反汇编和解压缩后反汇编。分析十亿个 128 字节缓冲区的结果表明,**反汇编的频率比成功解压缩高出 125 倍以上,比解压缩 *和* 反汇编都成功高出 350 倍以上。** 即使操纵数据以 *提高* 解压缩成功率,也没有改变这一结果。
进一步的分析表明,Thumb 指令随机出现的概率非常高(对于 2 字节序列约为 89%),这解释了结果。该研究还探讨了解压缩失败点,发现了 DEFLATE 头部和 Huffman 树有效性方面的问题。
该代码利用 Zig 的高效构建系统进行 Capstone 集成,运行速度很快——在普通硬件上大约 30 分钟内处理十亿个缓冲区。作者得出结论,Thumb 的代码密度使得有效的指令序列比有效的压缩数据更容易随机出现。完整的代码和数据可在 GitHub 上获取。
Homebrew 正在弃用 `--no-quarantine` 标志,该标志允许用户绕过 macOS 的 Gatekeeper 安全功能来运行未签名的应用程序。这一决定源于苹果日益增强的安全措施,尤其是在 Apple silicon Mac 上,它们*需要*有效的签名,以及苹果和 Homebrew 都已结束对 Intel 的支持。 目前,该标志主要用于覆盖 macOS 安全设置,而 Homebrew 积极劝阻这种做法。所有 cask 必须通过 Gatekeeper 检查的截止日期为 2026 年 9 月 1 日,因此继续维护该标志已无必要。 移除 `--no-quarantine` 将通过防止轻易绕过操作系统级别的保护来增强用户安全,并与苹果未来的平台方向保持一致。没有考虑替代方案,因为趋势是朝着更强的安全性和签名要求发展。此更改为用户提供了充足的时间来调整工作流程,然后再完全移除该标志。
## 旅行者1号:深空历史性里程碑 到2026年末,美国宇航局的旅行者1号探测器将成为第一个距离地球一光日——259亿公里——的人造物体,这一壮举历时近50年。旅行者1号于1977年发射,已经打破多项纪录,成为第一个进入星际空间并超越日球层探测器。 目前,旅行者1号距离地球169.5天文单位,信号需要超过23小时才能到达探测器。虽然以大约61,198公里/小时的速度飞行,但要将这一光距翻倍,也需要超过一年时间。这一里程碑凸显了太空的巨大尺度和当前旅行速度的局限性——即使以阿波罗10号的最高速度,也需要155天才能到达太阳。 旅行者1号的旅程不会随着这一成就而结束。它将继续穿过奥尔特云(可能持续数万年),预计在大约4万年后与格利泽445星进行近距离接触,比它离我们的太阳更近。最终,这艘探测器将在宇宙中漂流数十亿年,携带它的金唱片作为来自人类的信息。
该网站受到“阿努比斯”系统的保护,该系统旨在阻止人工智能公司过度抓取其内容。抓取会导致网站对所有用户不可用,而阿努比斯的目标是在可访问性和保护之间取得平衡。 阿努比斯通过要求访问者付出少量计算成本来工作——类似于反垃圾邮件技术。对于个人用户来说,这种成本可以忽略不计,但对于大规模抓取操作来说,它会变得显著且昂贵。 目前,阿努比斯可能会偶尔影响合法用户,但这是一种临时解决方案。开发者正在研究更精确的方法来识别和阻止用于抓取的自动化“无头浏览器”,从而最大限度地减少对真实访问者的干扰。使用像JShelter这样的JavaScript阻止插件的用户可能需要为该网站禁用它们,以确保正常功能。
 ## N键连打与按键冲突:总结
N键连打 (NKRO) 定义了键盘能够准确记录的同時按键数量。标准键盘通常具有6键连打,限制了同时输入。完全NKRO意味着*任意*数量的按键都可以被按下并正确记录。
**按键冲突** (Key ghosting) 发生在键盘由于内部电路的限制而错误地记录按键时。为了对抗这个问题,一些键盘具有“防冲突”技术——通常是一种软件解决方法,例如微软的SideWinder X4,它可以报告高达26个同时按键——但这并非真正的硬件NKRO。
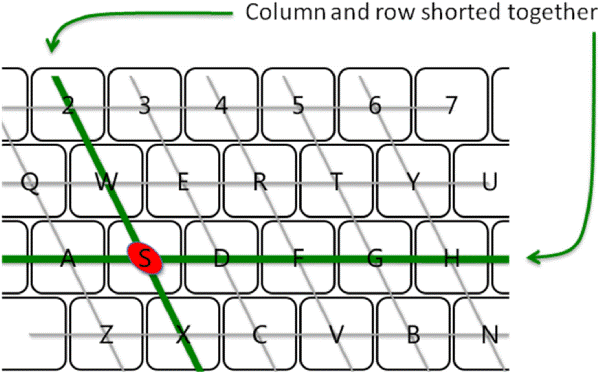
大多数键盘使用按键下方的网格系统来降低成本,这可能导致在同一行或列的按键被按下时发生按键冲突。虽然USB *可以* 处理完全NKRO,但许多默认限制为6键。较旧的PS/2连接通常支持完全NKRO。
完全NKRO对于特定应用至关重要,例如速记、盲文输入和高级游戏,在这些应用中,复杂的按键组合很常见。测试键盘的连打能力很简单:同时按住两个Shift键,然后尝试输入其他字母——如果有些字母没有被记录,则存在按键冲突。
## N键连打与按键冲突:总结
N键连打 (NKRO) 定义了键盘能够准确记录的同時按键数量。标准键盘通常具有6键连打,限制了同时输入。完全NKRO意味着*任意*数量的按键都可以被按下并正确记录。
**按键冲突** (Key ghosting) 发生在键盘由于内部电路的限制而错误地记录按键时。为了对抗这个问题,一些键盘具有“防冲突”技术——通常是一种软件解决方法,例如微软的SideWinder X4,它可以报告高达26个同时按键——但这并非真正的硬件NKRO。
大多数键盘使用按键下方的网格系统来降低成本,这可能导致在同一行或列的按键被按下时发生按键冲突。虽然USB *可以* 处理完全NKRO,但许多默认限制为6键。较旧的PS/2连接通常支持完全NKRO。
完全NKRO对于特定应用至关重要,例如速记、盲文输入和高级游戏,在这些应用中,复杂的按键组合很常见。测试键盘的连打能力很简单:同时按住两个Shift键,然后尝试输入其他字母——如果有些字母没有被记录,则存在按键冲突。
启用 JavaScript 和 Cookie 以继续。
## 大理石:生成式世界模型现已发布 大理石,一款尖端的人工智能世界模型,现已全面发布,它能赋予用户从简单的文本、图像、视频甚至粗略的3D布局中创建和互动于细节丰富的3D世界的能力。这种“多模态”方法允许进行广泛的创意控制——世界可以被完全生成、交互式编辑、扩展或由多个来源组合而成。 主要功能包括**Chisel**,一个用于精确3D雕刻的工具,以及扩展现有世界以创建更大、更详细环境的能力。导出选项包括高斯飞溅、网格和带有动态元素的增强视频。 **Marble Labs** 作为一个创意中心,展示了游戏、VFX、设计和机器人等领域的创新应用,并为所有级别的用户提供教程和文档。 此次发布代表着“空间智能”方面的一个重要步骤——即理解和模拟我们周围世界的AI。虽然目前专注于创建和编辑,但未来的开发目标是实现对这些生成世界内的无缝交互,以应用于模拟和机器人等领域。 立即在 [marble.worldlabs.ai](http://marble.worldlabs.ai) 开始构建您自己的3D世界!
这篇日记记录了作者因父亲突发心脏病去世的经历。在接到母亲越来越紧急的电话后,作者赶往医院,却发现父亲已经去世。 这场悲剧因等待了30分钟却始终未能等到救护车而更加令人痛心。尽管多次拨打911,调度员仍然建议等待,即使父亲正在遭受剧烈疼痛。家人最终自己开车将他送往医院,但他却在急诊室门口几步之遥的地方去世了。 作者难以接受这种毫无意义的情况,质疑导致父亲去世的系统性失误——缓慢的紧急响应、根深蒂固的等待救护车的观念,以及对这些缺陷令人沮丧的接受。他们分享这个故事是为了警示他人,不确定这些问题是局部性的还是普遍存在的,但决心强调盲目遵守规程可能造成的致命后果。